We recently published a paper in which we describe a new mesh of Schneiders’ pyramid (see images below). The paper describes two new algorithms used to construct it:
- A procedure to enumerate all hexahedral meshes with a specific boundary
- A procedure which locally modifies a hexahedral mesh to reduce the number of hexahedra without changing the boundary.
Our implementation of the algorithms described in the paper and our results can be downloaded below.
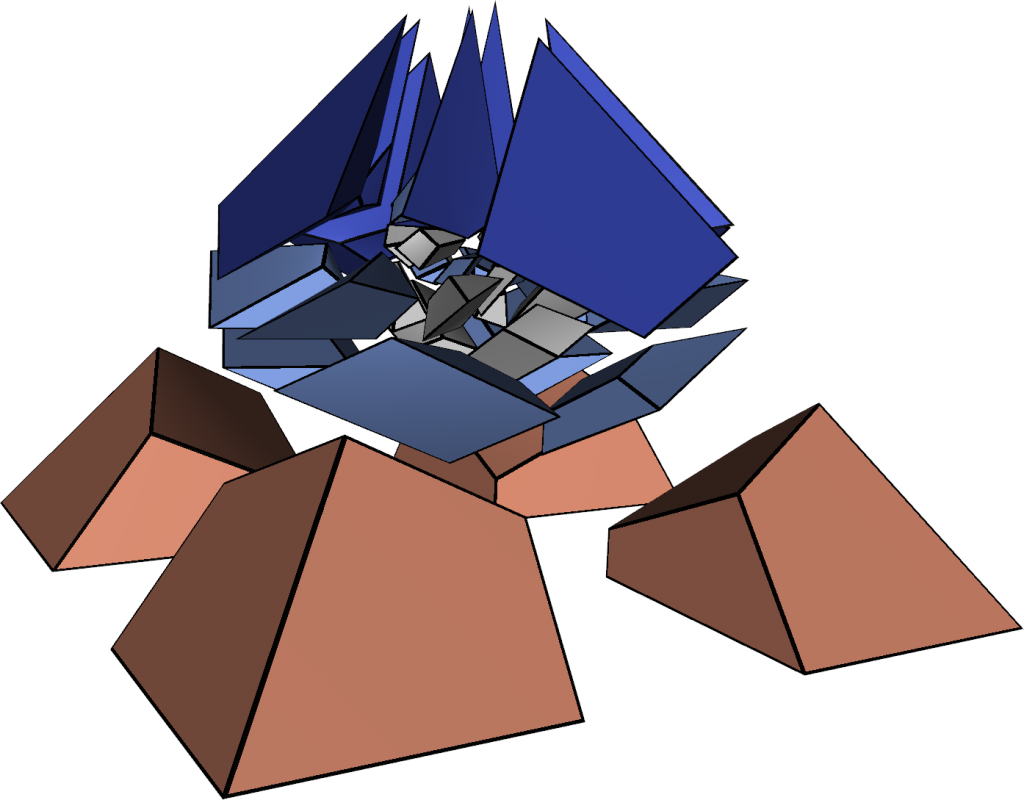

Abstract: This paper shows that constraint programming techniques can successfully be used to solve challenging hex-meshing problems. Schneiders’ pyramid is a square-based pyramid whose facets are subdivided into three or four quadrangles by adding vertices at edge midpoints and facet centroids. In this paper, we prove that Schneiders’ pyramid has no hexahedral meshes with fewer than 18 interior vertices and 17 hexahedra, and introduce a valid mesh with 44 hexahedra. We also construct the smallest known mesh of the octagonal spindle, with 40 hexahedra and 42 interior vertices. These results were obtained through a general purpose algorithm that computes the hexahedral meshes conformal to a given quadrilateral surface boundary. The lower bound for Schneiders’pyramid is obtained by exhaustively listing the hexahedral meshes with up to 17 interior vertices and which have the same boundary as the pyramid. Our 44-element mesh is obtained by modifying a prior solution with 88 hexahedra. The number of elements was reduced using an algorithm which locally simplifies groups of hexahedra. Given the boundary of such a group, our algorithm is used to find a mesh of its interior that has fewer elements than the initial subdivision. The resulting mesh is untangled to obtain a valid hexahedral mesh.
