Quad layouts with high valence singularities for flexible quad meshing

Authors: Jovana Jezdimirović, Alexandre Chemin, Maxence Reberol, François Henrotte, Jean-François Remacle

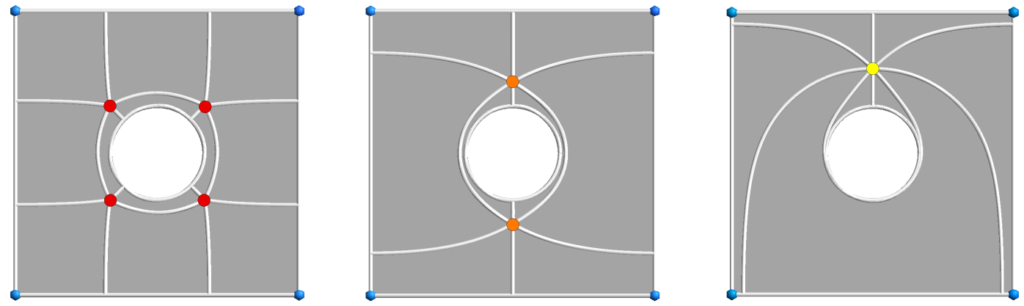
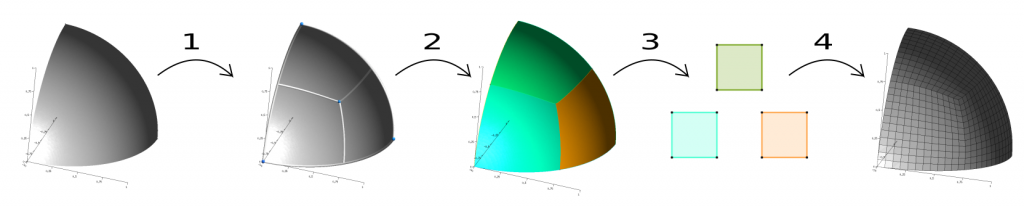
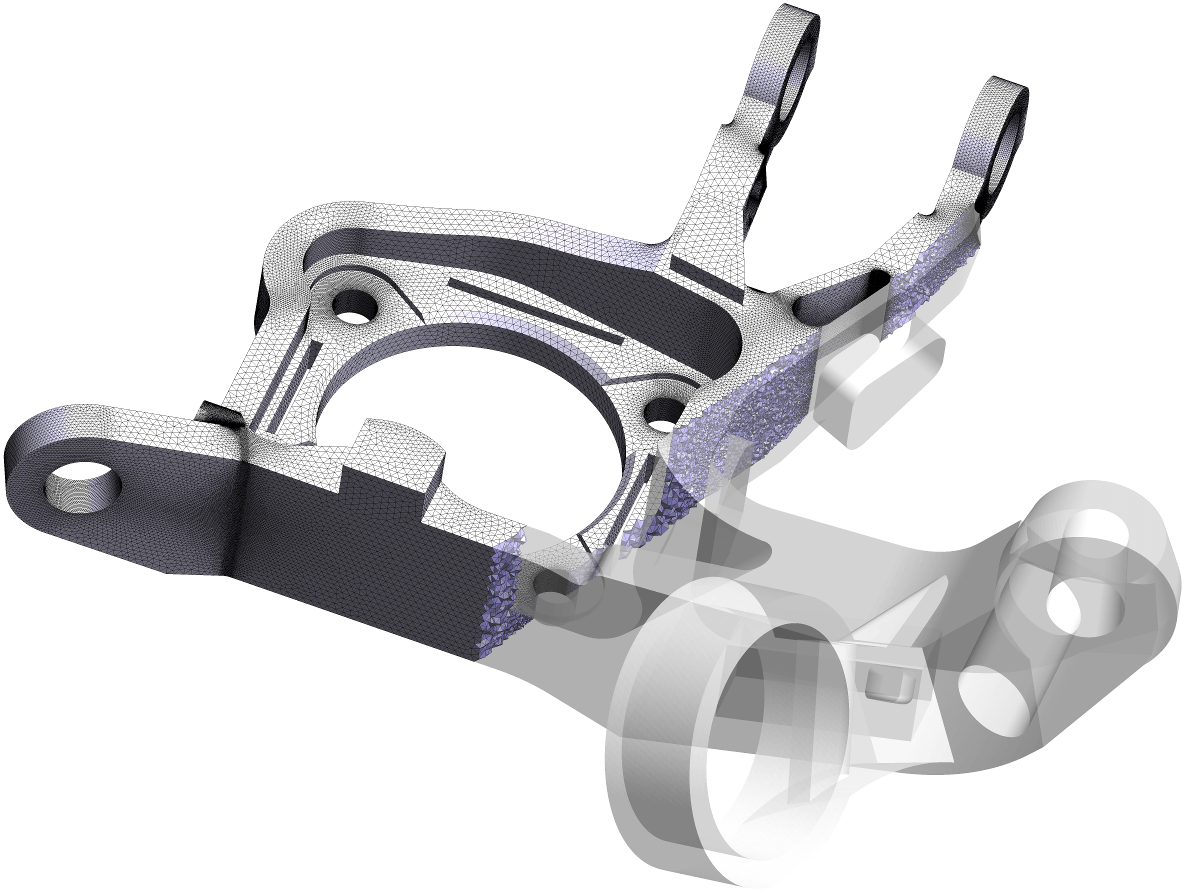
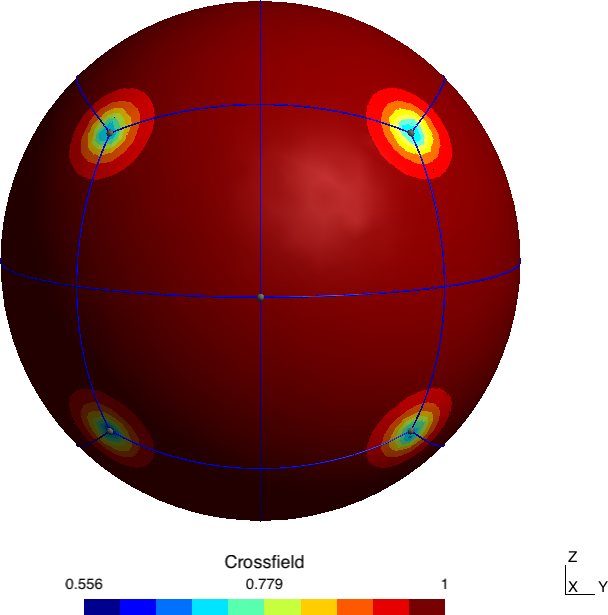
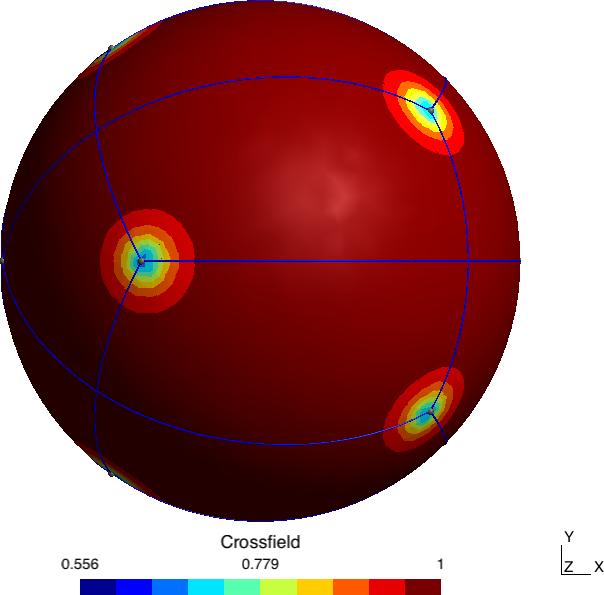
Abstract: A novel algorithm that produces a quad layout based on an imposed set of singularities is proposed. In this paper, we either use singularities that appear naturally, e.g., by minimizing Ginzburg-Landau energy, or use as an input user-defined singularity pattern, possibly with high valence singularities that do not appear naturally in cross-field computations. The first contribution of the paper is the development of a formulation that allows computing a cross-field from a given set of singularities through the resolution of two linear PDEs. Specific mesh refinement is applied at the vicinity of singularities to accommodate the large gradients of cross directions that appear in the vicinity of singularities of high valence. The paper’s second contribution is a correction scheme that repairs limit cycles and/or non-quadrilateral patches. Finally, a high-quality block-structured quad mesh is generated from the quad layout and per-partition parametrization.

Paper in proceedings of the 29th International Meshing Roundtable

FRAMES2020 workshop

Online event (free), December 9, 2020

The goal of the FRAMES workshop is to gather both theoretical (computer science & applied mathematics) and practical (engineering & industry) specialists in meshing.

The second edition is a small workshop jointly organized by the Computer Graphics Group from University of Bern, the Pixel team from INRIA/Loria and the Hextreme team from UCLouvain. Attendance is free and open to the public.

See the workshop webpage for more information:
https://www.hextreme.eu/frames2020/

Update: the recordings of the talks are now available on Youtube (see the workshop webpage).

Multi-block decomposition and meshing of 2D domain using Ginzburg-Landau PDE

Authors: Jovana Jezdimirović, Alexandre Chemin, Jean François Remacle

Abstract: An in-depth method to generate multi-block decomposition of the arbitrary 2D domain using 2D cross fields solution of Ginzburg-Landau partial differential equation (PDE) is presented. It is relied on parameterization of multi-block decomposition of the domain, obtained by using particular PDE for the purpose of generating direction fields, appropriate number and localization of singular points and their separatrices. We have proved that solutions of particular PDE imply locally integrable vector fields and have adequate distribution of singularities, advocating its usage. Multi-block graph was generated by the separatrices and extraordinary vertices of the domain (singularities, corners and separatrices intersections) and obtained blocks were parameterized/remeshed. As a result, a mechanism to obtain multi-block structured all-quad mesh in automatic manner is developed.

  • Paper (in proceedings of the 28th International Meshing Roundtable)
  • The code will soon be available in Gmsh

HXTSPR

Reviving the Search for Optimal Tetrahedralizations

  • unoptimized
  • smoothing + edge-removal
  • smoothing + edge-removal + SPR
https://git.immc.ucl.ac.be/hextreme/hxtspr

For the 28th International Meshing Roundtable held this year in Buffalo NY, we are revisiting an operation to find the optimal triangulation of a cavity (considering fixed points). This operation was named “Small Polyhedron Reconnection” (SPR) by Liu et al. in their 2006 paper which introduced it. Our implementation contains various optimizations, that differs from the optimization that Liu et al. described in their 2009 paper, notably adding memoization and robust exact intersection tests. We probably have to apologize that there is no reference or comparison to the optimized method of Liu et al. in our IMR paper. The unfortunate reasons for this are described in the README.md of our source code, available on Gitlab. Hope you enjoy(ed) our presentation at the IMR

FRAMES2019 workshop

First Workshop on Frame-based hex meshing
Université catholique de Louvain, Louvain-la-Neuve, July 1-2, 2019

The goal of the FRAMES workshop is to gather both theoretical (computer science & applied mathematics) and practical (engineering & industry) specialists in the field of frame-based hex-meshing, in view of numerical computations.

See the workshop webpage for more information:
https://www.hextreme.eu/frames2019/

Update: the slides are available

Finding Hexahedrizations for Small Quadrangulations of the Sphere

Authors: Kilian Verhetsel, Jeanne Pellerin, Jean-François Remacle


80%

(The meshes above can be rotated by clicking on them and dragging your cursor.)

Suppose you drew a set of n quadrangles on a sphere, covering its entirety. How many cubes do you need to fill the interior of that sphere? This question is surprisingly difficult to answer, even with only a few quadrangles (the case n = 8 is notoriously hard, and of the 3 cases where n = 10, only one is easy to solve).

Our contribution to SIGGRAPH 2019 shows that with n quadrangles on the boundary, 78n combinatorial cubes (or hexahedra) are always enough. This is a significant improvement over the previous upper bound: 5396n (Carbonera and Shepherd, 2010). Our result is based on a proof by Erickson (2014): we computed hexahedral meshes of the two base cases that it uses (shown above).

In most cases, there are significantly smaller solution. The paper gives an algorithm to search for such solutions. This was fast enough to compute hexahedral meshes for all 54,943 quadrangulations of up to 20 quadrangles for which a solution exists. The worst case required only 72 hexahedra.

Paper: One machine, one minute, three billion tetrahedra

We recently published a paper on fast parallel 3D Delaunay triangulation in the International Journal for Numerical Methods.

The paper describe how we designed a library able to compute up to 65 million tetrahedra per second*.

*on an AMD EPYC 7551 (2×32 core)

Paper: There are 174 subdivisions of the hexahedron into tetrahedra

A new paper was published, wherein we enumerate all possible ways to subdivide a hexahedron into tetrahedra, and which of those subdivisions can be realized geometrically in 3-dimensional space.

The paper will be presented at SIGGRAPH Asia 2018.

 

Paper: A 44-Element Mesh of Schneiders’ Pyramid

We recently published a paper in which we describe a new mesh of Schneiders’ pyramid (see images below). The paper describes two new algorithms used to construct it:

  1. A procedure to enumerate all hexahedral meshes with a specific boundary
  2. A procedure which locally modifies a hexahedral mesh to reduce the number of hexahedra without changing the boundary.

Our implementation of the algorithms described in the paper and our results can be downloaded below.

Abstract: This paper shows that constraint programming techniques can successfully be used to solve challenging hex-meshing problems. Schneiders’ pyramid is a square-based pyramid whose facets are subdivided into three or four quadrangles by adding vertices at edge midpoints and facet centroids. In this paper, we prove that Schneiders’ pyramid has no hexahedral meshes with fewer than 18 interior vertices and 17 hexahedra, and introduce a valid mesh with 44 hexahedra. We also construct the smallest known mesh of the octagonal spindle, with 40 hexahedra and 42 interior vertices. These results were obtained through a general purpose algorithm that computes the hexahedral meshes conformal to a given quadrilateral surface boundary. The lower bound for Schneiders’pyramid is obtained by exhaustively listing the hexahedral meshes with up to 17 interior vertices and which have the same boundary as the pyramid. Our 44-element mesh is obtained by modifying a prior solution with 88 hexahedra. The number of elements was reduced using an algorithm which locally simplifies groups of hexahedra. Given the boundary of such a group, our algorithm is used to find a mesh of its interior that has fewer elements than the initial subdivision. The resulting mesh is untangled to obtain a valid hexahedral mesh.

Paper: Computing cross fields, a PDE approach based on Ginzburg-Landau theory

We developed an innovative way to compute cross fields in order to spawn points which are consistent with a square grid. The mathematical background is built step by step to highlight the meaningful use of Ginzburg-Landau functional. An interesting result is obtained over the sphere: the anti-cube. The computation is extended to asterisk fields for equilateral triangular grid.