
The goal of the FRAMES workshop is to gather both theoretical (computer science & applied mathematics) and practical (engineering & industry) specialists in the field of frame-based hex-meshing, in view of numerical computations.
This first edition is organized at the Université catholique de Louvain (Belgium) by Jean-François Remacle and Maxence Reberol.
Presentations are by invitation only; attendance is free thanks to our generous sponsors.
The first day is dedicated to presentations and the second one to discussions.
| July 1st | July 2nd |
|---|---|
|
|
The state of the art in tetrahedral meshing has now reached a maturity
that makes it reasonably easy to mesh arbitrary shapes using existing
software. For hexahedral meshing, the situation is different, and
despite important advances, the state of the art is still far away from
a general and robust fully automatic solution.
At the moment there is no method capable of generating acceptable fully
hexahedral meshes automatically. The number of failure cases remains
important, even for simple objects that can exhibit some difficult
combinatorial aspects of the problem. There are many shapes virtually
impossible, or at least, very unobvious to mesh (even by hand!) with pure
hexahedral elements. For this reason, hexahedral-dominant meshing may be an
option worth investigating: by relaxing the problem, it still generates a valid
result in complicated case where full-hexahedral methods generally fail, at the
expense of introducing non-hexahedral elements such as tetrahedra, pyramids and
prisms.
Please note that the importance/utility of mixed element meshes is not clear
yet. What are mixed elements meshes useful for? It is widely admitted that
when it comes to simulation, there are cases when pure hexahedral meshes are
superior to tetrahedral meshes for several reasons (e.g. resolution, accuracy,
anisotropy). However, we need to answer to what extent a mixed element mesh
can admit non hexahedral elements in order to be still preferred to, say, a
pure tetrahedral mesh.
In this talk we will present our thoughts on recent advances in this domain,
including few research ideas on how to improve global parameterizations and how
to make global parameterizations useful for real-life objects posing numerous
challenges.
Automatically generating hexahedral meshes is a notoriously challenging task, specifically if alignment to freeform surfaces in combination with high mesh regularity and low distorted elements is required. Novel algorithms based on global optimization rely on the construction of integer-grid maps, which pull back a Cartesian grid of integer isolines from a 3D domain onto a structure aligned hexahedral mesh. Such global optimization algorithms do not suffer from limitations known from local advancing front methods, as for instance a high rate of irregularity, and enable meshes comparable to manually designed ones by finding a good compromise between regularity and element distortion. The key to efficiently finding high-quality solutions are 3D frame fields that are employed to optimize the orientation and sizing of mesh elements globally. While initial results are promising, a major open challenge consists in guaranteeing that the frame field has meshable topology and is close to being integrable. In my talk, I will give an overview of the state of the art and discuss the strengths and weaknesses of available algorithms, including open challenges for hexahedral meshing.
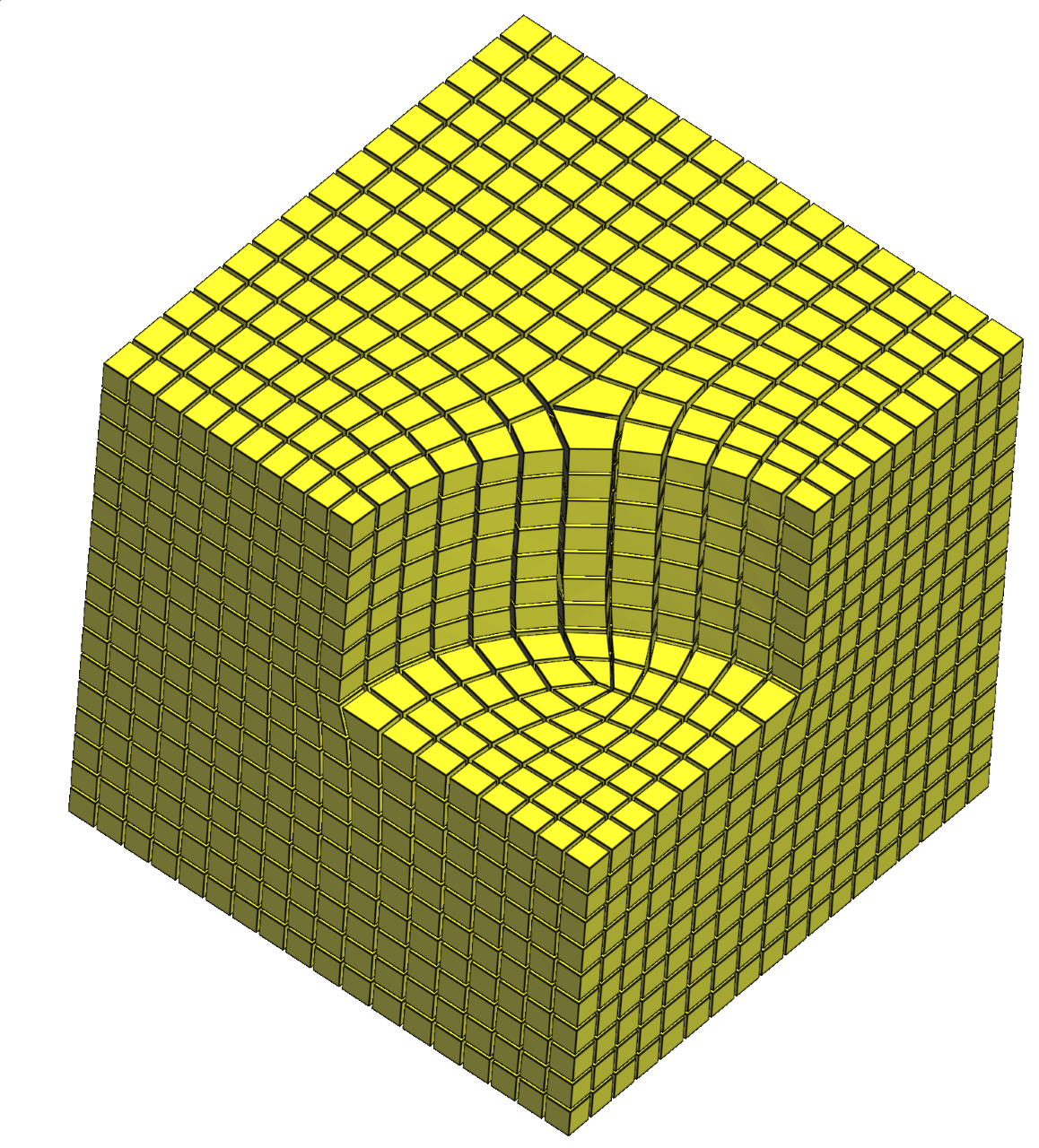
Hexahedral mesh generation is challenging even topologically. This poses
challenges that are not faced by tetrahedral meshing techniques: certain small
cavities are very difficult to mesh using hexahedra; cavities with very similar
boundary may require hexahedral meshes with completely different levels of
complexity.
In this presentation, we'll look at known theoretical results about topological
hexahedral mesh generation, recent advances in finding practical topological
meshes for small cavities, and some of the implications of those results for
general hexahedral mesh generation.
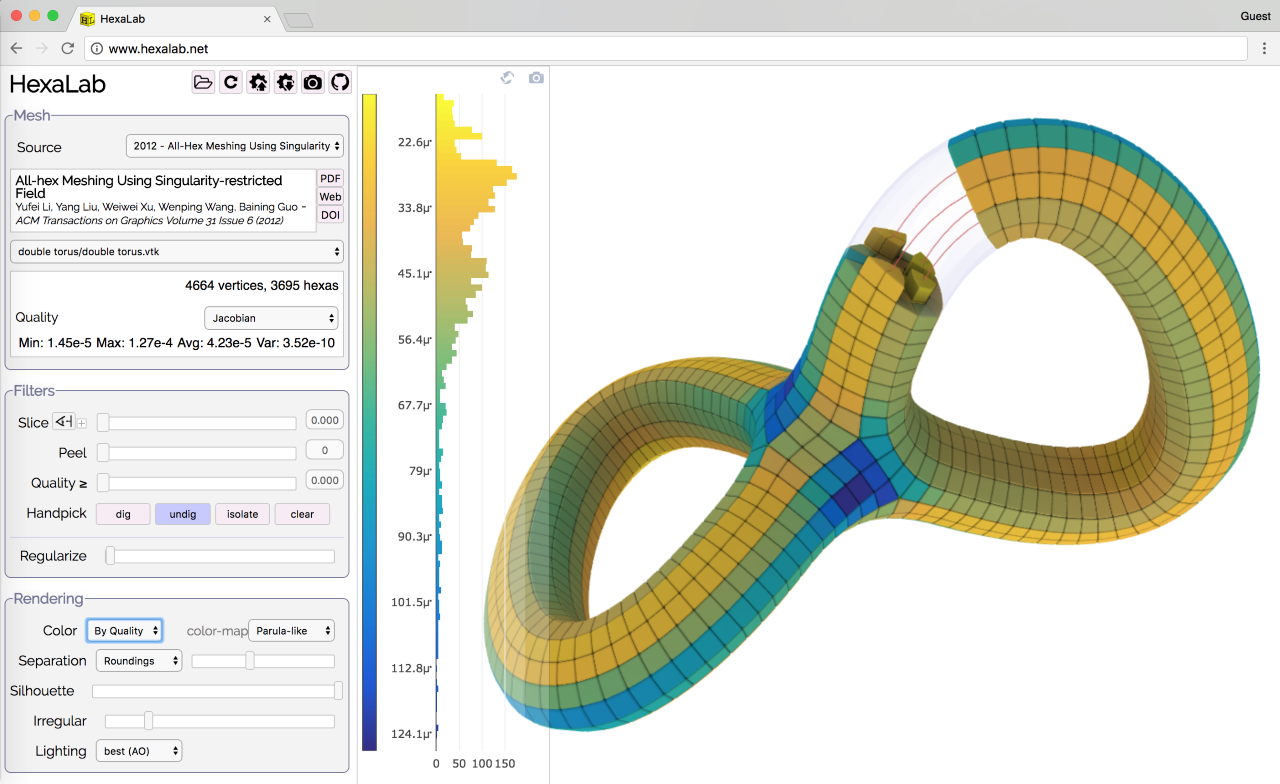
Hexahedral meshes are discretized volumetric 3D models commonly employed in applications such as Finite Elements Methods or other physical simulations. Their construction is recognized to be a challenging field of research in the context of geometry processing and FEM. This talk addresses the task of their real-time visualization, exploration, and assessment. For this purpose, we present a tool-set targeted at practitioners and scholars, which can be used to readily assess quality of the meshing and consequently the usability of the model for simulation. This can be used by researchers involved in the design of hexa-mesh generation algorithms to perform a detailed visual analysis of the obtained results, and compare them to previous and concurrent solutions. The system is offered as a easily accessible online suite, which doubles as a portal to a growing benchmark consisting of publicly available datasets produced with recent techniques.
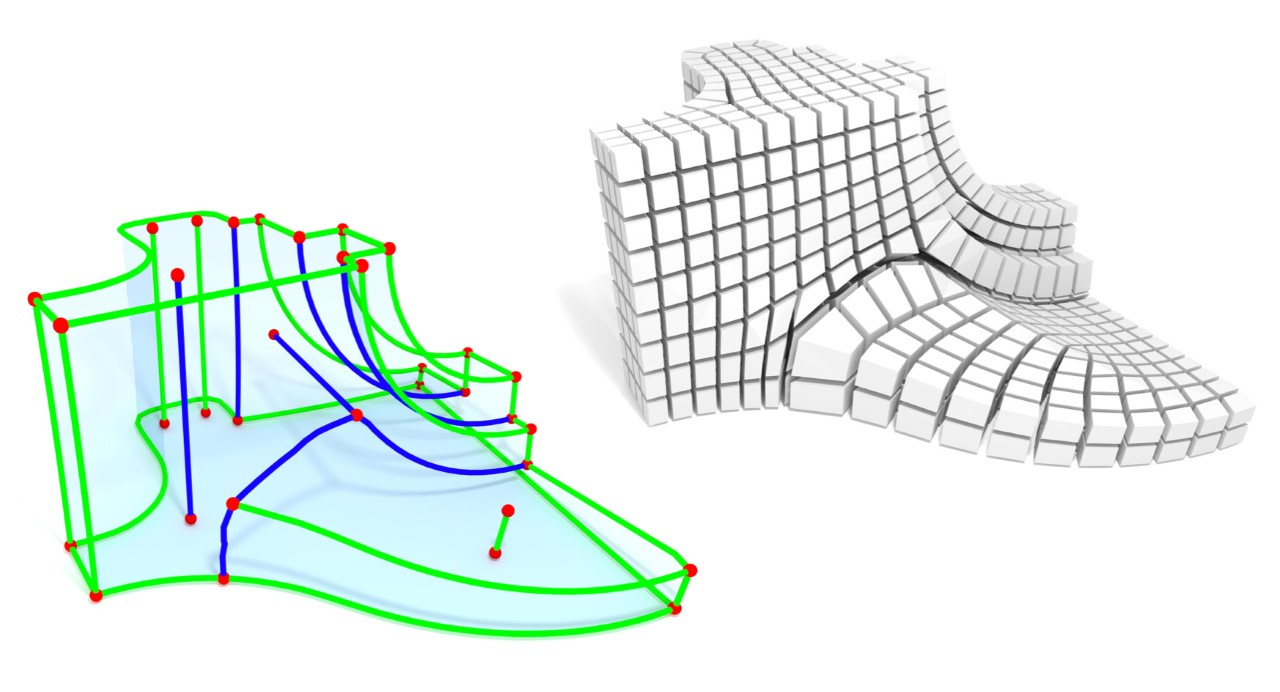
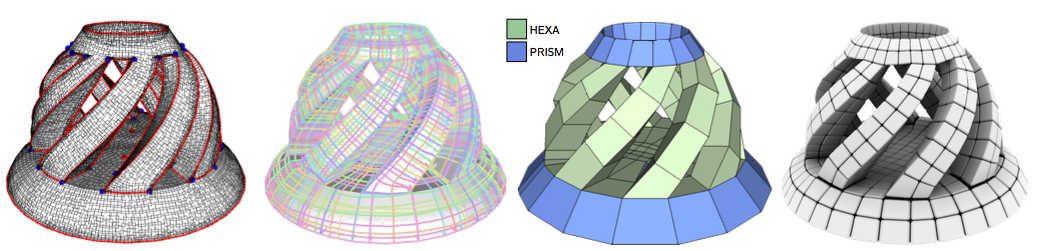
We present a new fully automatic block-decomposition hexahedral meshing algorithm capable of producing high-quality meshes that strictly preserve feature curve networks on the input surface and align with an input surface cross-field. We produce all-hex meshes on the vast majority of inputs and introduce localized non-hex elements only when the surface feature network necessitates those. The input to our framework is a closed surface with a collection of geometric or user-demarcated feature curves and a feature-aligned surface cross-field. Its output is a compact set of blocks whose edges interpolate these features and are loosely aligned with this cross-field. We obtain this block decomposition by cutting the input model using a collection of simple cutting surfaces bounded by closed surface loops. The set of cutting loops spans the input feature curves, ensuring feature preservation, and is obtained using a field-space sampling process. The computed loops are uniformly distributed across the surface, cross orthogonally, and are loosely aligned with the cross-field directions, inducing the desired block decomposition. We validate our method by applying it to a large range of complex inputs and comparing our results to those produced by state-of-the-art alternatives. Contrary to prior approaches, our framework consistently produces high-quality field aligned meshes while strictly preserving geometric or user-specified surface features.
A possible strategy to construct cross-fields that are as smooth as possible is to make them harmonic maps, which are generalization of harmonic functions and geodesics on a manifold. Minimizing harmonic maps are reasonably well-behaved and regular, although they can and do exhibit singularities for topological and energetical reasons. In general, boundary conditions on the cross-fields induce topological obstructions to a continuous or finite-Dirichlet-energy cross-field extension that make impossible the existence of a minimizing harmonic extension. A Ginzburg–Landau relaxation replaces the non-linear target-manifold constraint of a penalization when the extension is away from the constraint manifold. When the penalization becomes stronger, the solutions tend asymptotically to harmonic maps outside a set of codimension 2. The position and the topological structure of singularities solves a minimization problem that can be written in terms of singularities. Since the fundamental group of the space of cross-fields is non-abelian, the combination rules for singularities are somehow involved and cannot be directly described with decompositions in the fundamental group. The fundamental group of the space of cross-fields also suggest the possibility that 120° cannot be ruled out. The angles between singularity lines at vertices satisfy some condition.
The hexahedral meshing problem is the volumetric analog of the quad meshing problem, with analogous applications in finite element modeling. One might expect that frame field–based methods, which have proven effective in quad meshing, would extend naturally to the volumetric case. Unfortunately, several problems arise in attempting this extension. The geometry of frames becomes significantly more complicated, making optimization over frames more challenging. Moreover, field and mesh topology is far more complicated in 3D due to non-commutative symmetries. I will discuss our recent work (joint with David Bommes and Justin Solomon), in which we examine the geometry of two different spaces of frames and develop tailored optimization techniques to achieve state-of-the-art fields. Next, time permitting, I will detail some observations (joint with Paul Zhang) about integrability and meshability of frame fields. Finally, I will talk about tantalizing insights we have gleaned from the physics of topological defects in ordered media.
There is great current interest in using cross fields for 2D quad
meshing and frame fields for hexahedral meshing, but one of the issues
in 3D is in identifying a valid block topology and network of mesh
singularities. Another technique that has had some success in the past
was to use the medial axis transform of the domain, which provides a
lower-dimensional skeleton of the object and identifies parts of the
boundary in geometric proximity, to partition the domain into simpler
meshable regions.
Recent experiments have used cross and frame fields generated on top of
the medial axis of the domain. By generating frames and cross fields on
medial vertices, edges and faces based on touching vectors, a
directional field is constructed on top of the medial object. Critical
lines in the domain called, singularity lines, are then identified.
Starting from these lines, a complete line network is created on the
interior of the domain. This network is extruded to the boundary in
order to create, together with singularity lines, the boundary of
partitioning surfaces. The resulting partition surfaces are then used
to decompose the domain into regions appropriate for generating a
high-quality hexahedral mesh.
In this talk, we explore the limitations of current frame-field formulations for hexahedral meshing. Many issues stem from the boundary conditions. For CAD models, the common approach is to impose frames on feature curves and to impose tangency of the frames (one direction) on smooth surfaces. We show that CAD feature curves can induce valence 3-5 curves in the singularity graph, which are not compatible with hex-meshing. We propose to eliminate them by snapping the invalid singular curves on the boundary and recomputing a corrected frame-field with new boundary conditions, which are no longer tangent to the surface. We also discuss the case of complicated boundary corners (e.g. pyramid apex), where it does not make sense to impose frames.
There is no registration fee for the FRAMES workshop, but registration is mandatory through the following google form. (No email confirmation is sent when you submit the form.)
The organizers and the sponsors will support all lunches. Travel expenses, lodging and dinners are at the participants' own charge.
The workshop will be held at the Université catholique de Louvain in Louvain-la-Neuve (Belgium), in the Euler Building:
UCLouvain, Bâtiment Euler
The welcome coffee, the lunches and the coffee pauses will take place in the hall
of the Euler building (ground floor)
(maps).
The conference room for the first day is located at the first floor of Maxwell Building, in the "Shannon" seminar room
(accessible from the Euler building)
(maps).
The discussions of the second day will take place in room A002, at the ground floor of the Euler building.
(maps).
There are two hotels in Louvain-la-Neuve (walking distance to the workshop):
After the first workshop session (6pm) and before the banquet (8pm), you can relax at the Beer bar.
The banquet will take place at Louvain House (Traverse Comte Yves du Monceau (ex Terrasse de l'Aula), 1348 Louvain-la-Neuve) (maps).
(walking distance from the hotels)
Free WiFi is available in the conference room through eduroam.

