Tag: meshing

A new paper was published, wherein we enumerate all possible ways to subdivide a hexahedron into tetrahedra, and which of those subdivisions can be realized geometrically in 3-dimensional space.

The paper will be presented at SIGGRAPH Asia 2018.

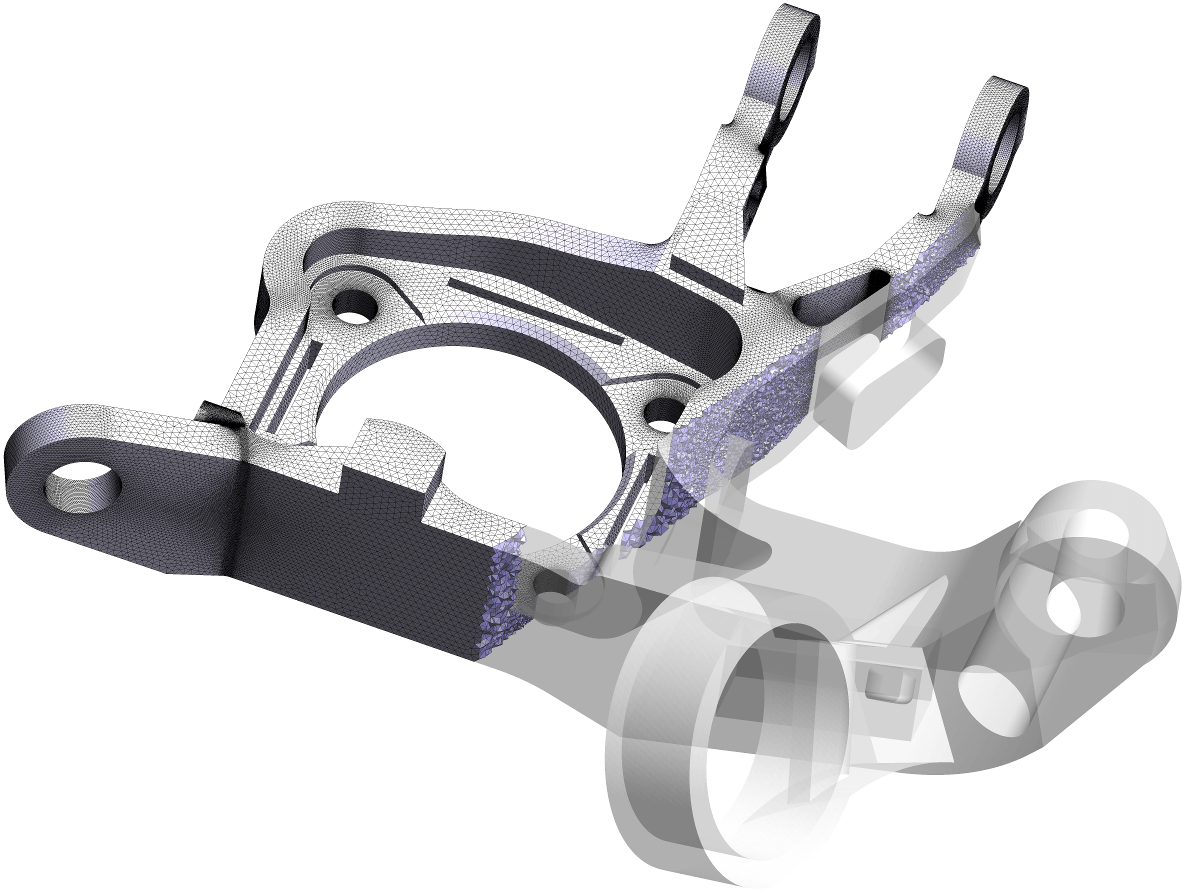
We recently published a paper in which we describe a new mesh of Schneiders’ pyramid (see images below). The paper describes two new algorithms used to construct it:

1. A procedure to enumerate all hexahedral meshes with a specific boundary
2. A procedure which locally modifies a hexahedral mesh to reduce the number of hexahedra without changing the boundary.

Our implementation of the algorithms described in the paper and our results can be downloaded below.

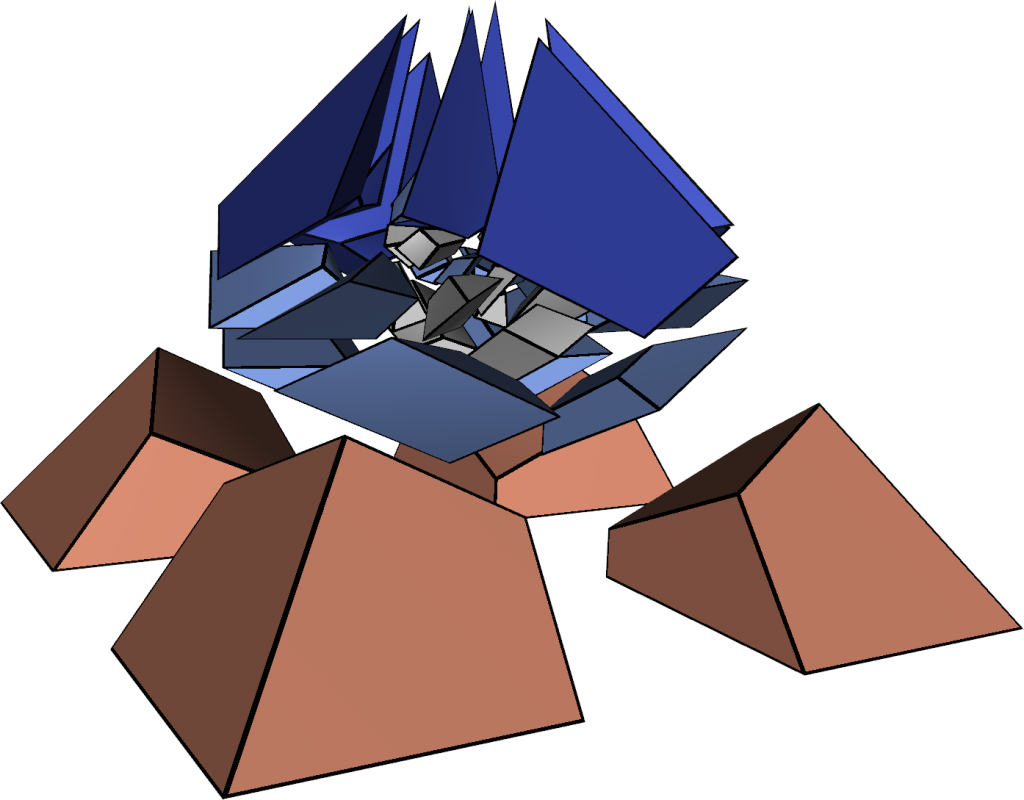
Abstract: This paper shows that constraint programming techniques can successfully be used to solve challenging hex-meshing problems. Schneiders’ pyramid is a square-based pyramid whose facets are subdivided into three or four quadrangles by adding vertices at edge midpoints and facet centroids. In this paper, we prove that Schneiders’ pyramid has no hexahedral meshes with fewer than 18 interior vertices and 17 hexahedra, and introduce a valid mesh with 44 hexahedra. We also construct the smallest known mesh of the octagonal spindle, with 40 hexahedra and 42 interior vertices. These results were obtained through a general purpose algorithm that computes the hexahedral meshes conformal to a given quadrilateral surface boundary. The lower bound for Schneiders’pyramid is obtained by exhaustively listing the hexahedral meshes with up to 17 interior vertices and which have the same boundary as the pyramid. Our 44-element mesh is obtained by modifying a prior solution with 88 hexahedra. The number of elements was reduced using an algorithm which locally simplifies groups of hexahedra. Given the boundary of such a group, our algorithm is used to find a mesh of its interior that has fewer elements than the initial subdivision. The resulting mesh is untangled to obtain a valid hexahedral mesh.

• Paper (from the proceedings of the 27th International Meshing Roundtable)
• Slides from the presentation at the 27th International Meshing Roundtable
• 44-element mesh of the pyramid
• 40-element mesh of the octagonal spindle
• Source code (GPL-licensed)

We developed a method to very efficiently combine the elements of a tetrahedral mesh into hexahedra.  The new vertex based algorithm builds all the feasible potential hexahedra  under given quality constraints. Around 3 millions of potential hexahedra are generated in 10 seconds. A greedy combination is used to compute the final hex-dominant mesh.

• The paper is available on arXiv:   arxiv.org/abs/1705.02451.
• The C++ code will soon be available in Gmsh.
• Input tetrahedral meshes are available here.