Tag: tool

Paper: Computing cross fields, a PDE approach based on Ginzburg-Landau theory

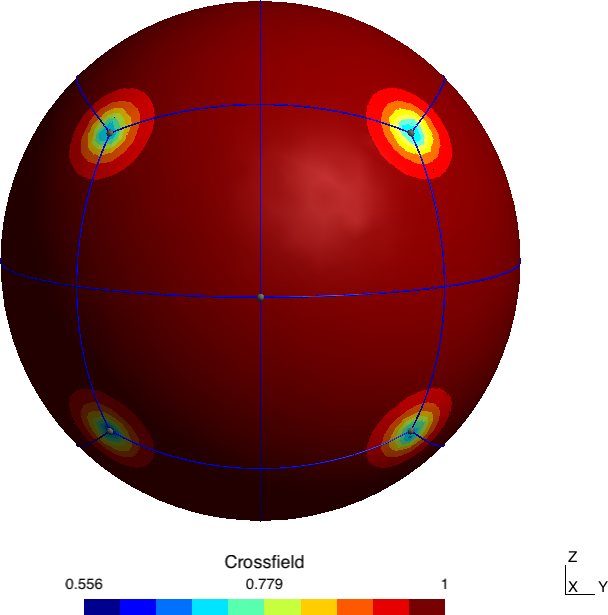
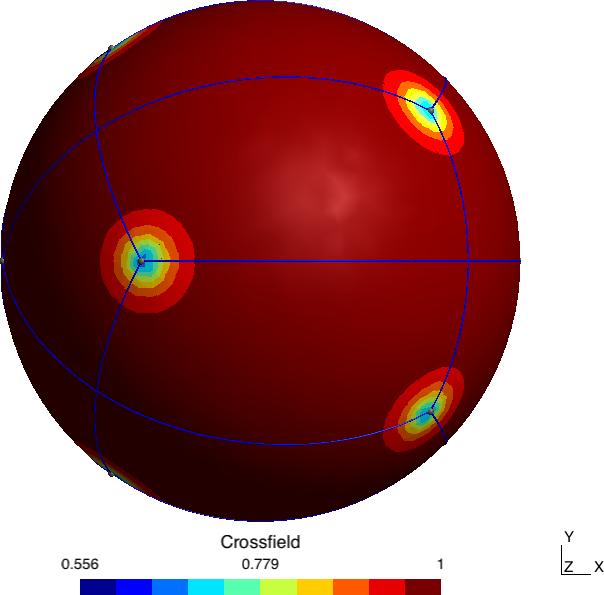
We developed an innovative way to compute cross fields in order to spawn points which are consistent with a square grid. The mathematical background is built step by step to highlight the meaningful use of Ginzburg-Landau functional. An interesting result is obtained over the sphere: the anti-cube. The computation is extended to asterisk fields for equilateral triangular grid.

Beaufort, Pierre-Alexandre et al. « Computing cross fields A PDE approach based on the Ginzburg-Landau theory », Procedia Engineering, vol. 203, 2017, p. 219‑31. <https://doi.org/10.1016/j.proeng.2017.09.799>.

HXTSort

view on GitLab

view on gitlab
HXTSort – Hextreme Sorting Library

HXTSort is a single header library including lightning fast Parallel Radix Sort macros.

It can sort 400 million integers per second on a laptop’s  i7-6700HQ and up to 1 billion integers per second on a Intel® Xeon Phi™  7210 ( 1.30GHz).

 

HXTSort is a lot faster than qsort
Because HXTSORT32_UNIFORM does not always pick the best underlying algorithm on the core i7, we manually chose the best of LSB32 and PARALLEL_HYBRID32.

It includes multiple  key-based algorithms for sorting data on any standard computer (single-node SMPs). It could also be a very good core algorithm for a MPI merge sort implementation for Clusters.

HXTSort will be used in our future Mesh Generation Library. A version of this library containing only a basic Mesher will be released soon.

Paper: Robust and efficient validation of the linear hexahedral element

We present a method to compute the true validity of hexahedra in an efficient manner. More than 6 million hexahedra are analyzed on a single core per second.

Johnen, Amaury, Jean-Christophe Weil et Jean-François Remacle. « Robust and Efficient Validation of Linear Hexahedral Elements », dans 26th International Meshing Roundtable, Barcelona, Spain, 2017.