Authors: Jovana Jezdimirović, Alexandre Chemin, Jean François Remacle
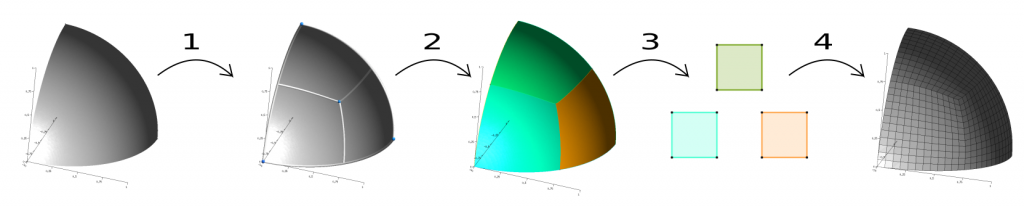
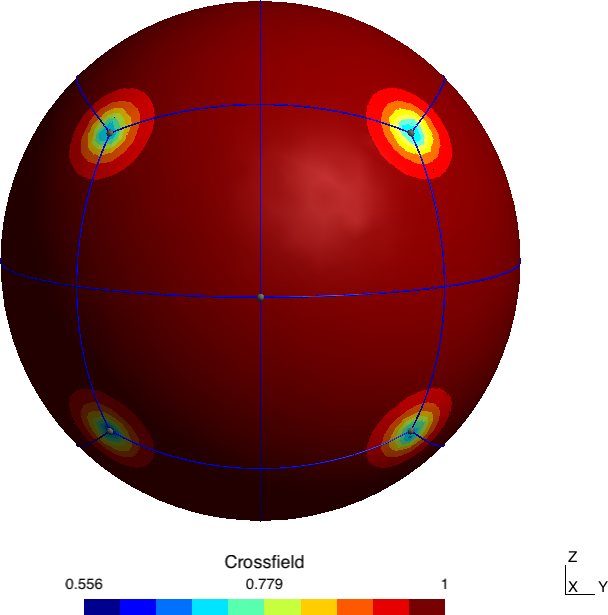
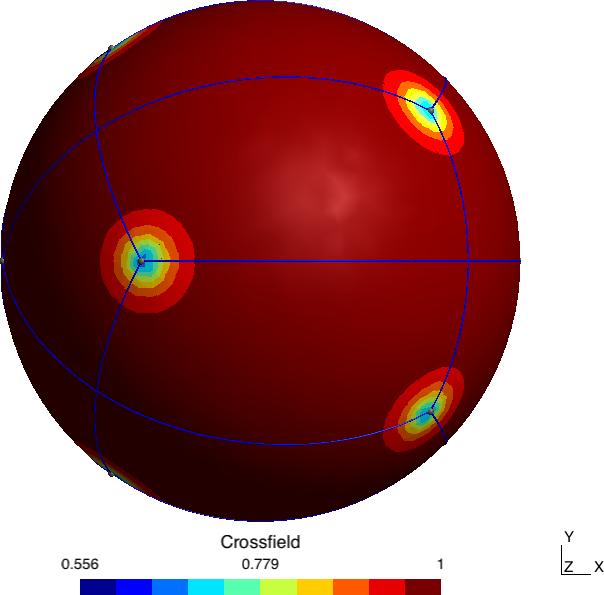
Abstract: An in-depth method to generate multi-block decomposition of the arbitrary 2D domain using 2D cross fields solution of Ginzburg-Landau partial differential equation (PDE) is presented. It is relied on parameterization of multi-block decomposition of the domain, obtained by using particular PDE for the purpose of generating direction fields, appropriate number and localization of singular points and their separatrices. We have proved that solutions of particular PDE imply locally integrable vector fields and have adequate distribution of singularities, advocating its usage. Multi-block graph was generated by the separatrices and extraordinary vertices of the domain (singularities, corners and separatrices intersections) and obtained blocks were parameterized/remeshed. As a result, a mechanism to obtain multi-block structured all-quad mesh in automatic manner is developed.